Voortgang
{Score}/{MaxScore}
  1. Examentraining 2 Meetkunde vmbo-gt
  2. Serie driehoeken

Serie driehoeken

In het assenstelsel hieronder zie je een aantal gelijkvormige driehoeken. 
De driehoeken worden steeds groter en zijn genummerd met de nummers `1`, `2`, `3`, enzovoort.

Driehoek nummer `1` heeft als hoekpunten `A_1`, `B_1`  en  `C_1`.  
Driehoek nummer `2` heeft als hoekpunten `A_2`, `B_2`  en  `C_2`, enzovoort.
De volgende driehoeken uit deze serie ontstaan steeds op dezelfde manier. 

Schrijf de coördinaten van de hoekpunten `"A"_4`, `"B"_4` en `"C"_4` van driehoek nummer `4` op.

De coördinaten van `"A"_1` zijn (`1","3`).
In een groter assenstelsel kun je ook driehoeken met hogere nummers tekenen.

Schrijf de coördinaten van `"A"_12` op. Leg ook uit hoe je aan je antwoord komt.
 
Om de oppervlakte van driehoek `"A"_1``"B"_1``"C"_1` te berekenen, kun je een om de driehoek heen getekende rechthoek gebruiken. Zie de schets.

Elk hokje stelt `1`  `"cm"^2` voor.
De coördinaten van `"B"_1` zijn (`−1` ,`−(1)/(2)`).

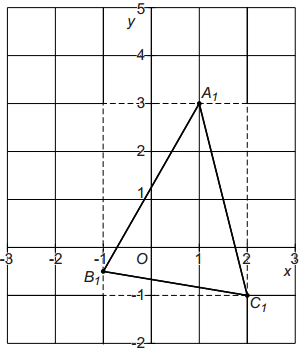
Laat met een berekening zien dat de oppervlakte van driehoek `"A"_1``"B"_1``"C"_1`
gelijk is aan `5","75`  `"cm"^2`.
Schrijf je berekening op.
Driehoek `"A"_6"B"_6"C"_6` is een vergroting van driehoek `"A"_1"B"_1"C"_1`.
De zijden van driehoek `"A"_6"B"_6"C"_6` zijn `6` keer zo groot als de zijden van driehoek `"A"_1"B"_1"C"_1`.

Bereken de oppervlakte van driehoek `"A"_6"B"_6"C"_6`. Schrijf je berekening op.

v1.12.0.0 Copyright © 2024 VO-next